计组Lab4 模拟cache设计

在做这个实验之前，我们需要掌握cache的基础知识~你可能需要知道的有

1. cache行，有效位，tag的概念和作用
2. cache直接映射，组相联映射，全相联映射的概念
3. LRU等cache替换原则

ps：访问cache的地址和访问主存的地址的数据是相同的，只是cache和主存解析这个地址的方式不同，如组相联cache的访问形式是tag,set,offset，而主存只会把这个地址拆成block(块号），offset的形式。

如果对cache的基础知识有些不了解~这里强推B站Beokayy_的视频，讲的非常细致！醍醐灌顶！！
带你彻底搞懂cache

Part 1 Cache模拟器实现

问ai就行（），如果扎实掌握cache基础知识的话其实很快就会理解（（
其实是我写不动了。。

提示：
用静态二维数组而非动态数组可以少写很多行代码
输出无前导0的16进制数，可以直接用 %llx，会方便许多

这里主要关注实验二

Part2 矩阵转置优化

这个实验让我们干什么？

首先我们有一个s = 4（一共2^4 = 16组），E = 1(每个组只有一行，相当于直接映射)，b = 5(一行2^5 =32个字节，即8个int)的cache

我们接下来需要实现一个矩阵转置函数，使得cache的miss率尽量小

为啥直接转不行啊

我们想到反转一个M行N列矩阵最直接的方法是

int i, j;
for(i = 0; i < M; i++){
	for(j = 0; j < N; j++){
		B[j][i] = A[i][j];
	}
}

提交测评，发现16 * 16矩阵的miss次数达到了305次，而32 * 32矩阵的次数更是达到了惊人的1211次，和要求的次数差得甚远

为什么会这样呢🤔

我们这里拿16 * 16的矩阵为例，看看这段代码是怎么运行的

代码的逻辑是，先把A的第1行放到B的第1列，再把A的第2行放到B的第2列，等等等。

A矩阵长这样（有点丑请见谅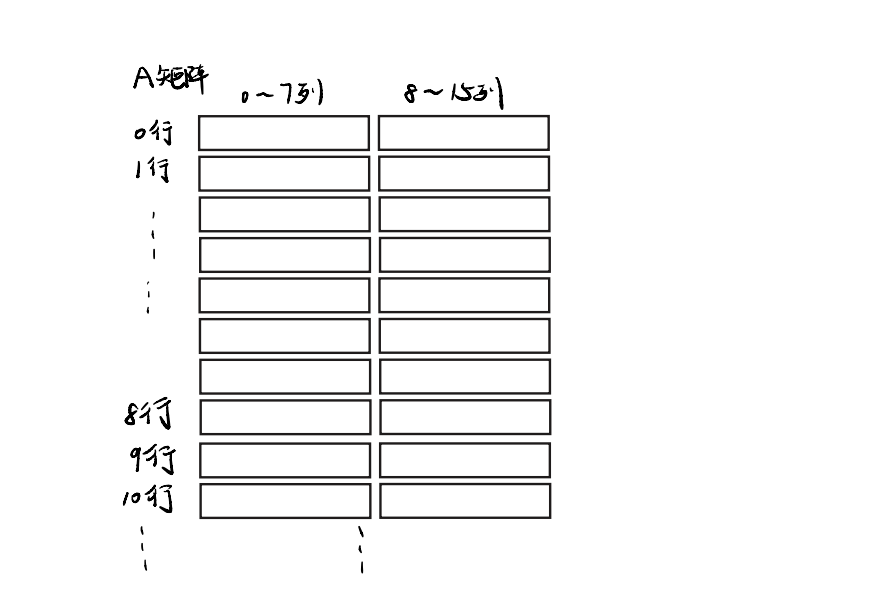

至于为什么我们把A矩阵画成这样这样，是因为cache的一行能放8个int，也就是说每次读到A[i][j]的时候，他会把A[i][j]所在第i行连着的8个元素一同装进cache，如存A[3][5]时会把A[3][0:8]的所有元素都装进cache。那我们就把8个画在一起吧~。

ps:A[0][0:8]表示A[0][0]~A[0][7]，简写一下防止我累死

还记得我们的cache是直接映射的吗，这也就是说，每个A[i][0:8]和A[i][9:16]映射到cache中的位置是固定的，我们这里不妨假设A[0][0:7]映射到了cache的第0行，那么也就是说，这些A矩阵在cache的映射关系如下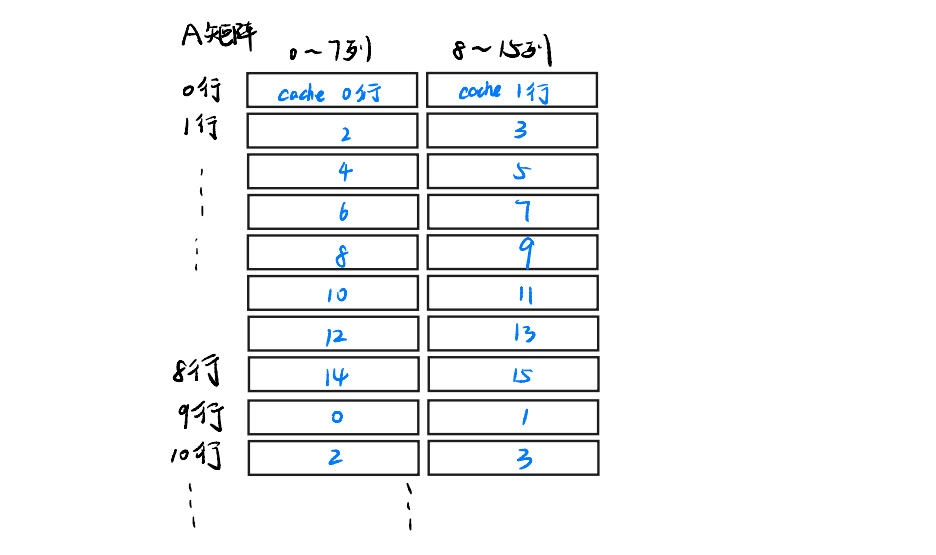

蓝字表示，数组的八个元素映射到的cache的固定位置

类似的，B矩阵的映射关系同理。在这里，为了方便说明，我们也假设A和B两个矩阵在内存上是连续的，这样B[0][0:8]同样也会映射到cache的第0行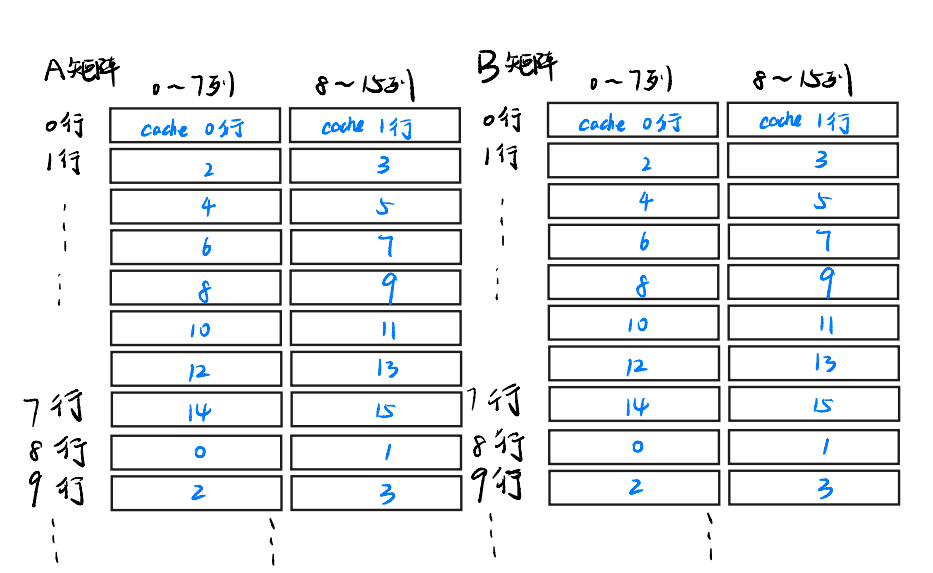

理解了映射关系，我们就可以分析刚才的那段代码了，首先，当i = 0, j = 0时，会先访问A[0][0],这样，他就会把A[0][0:8]全部扔到cache的第0行，miss次数变成了1。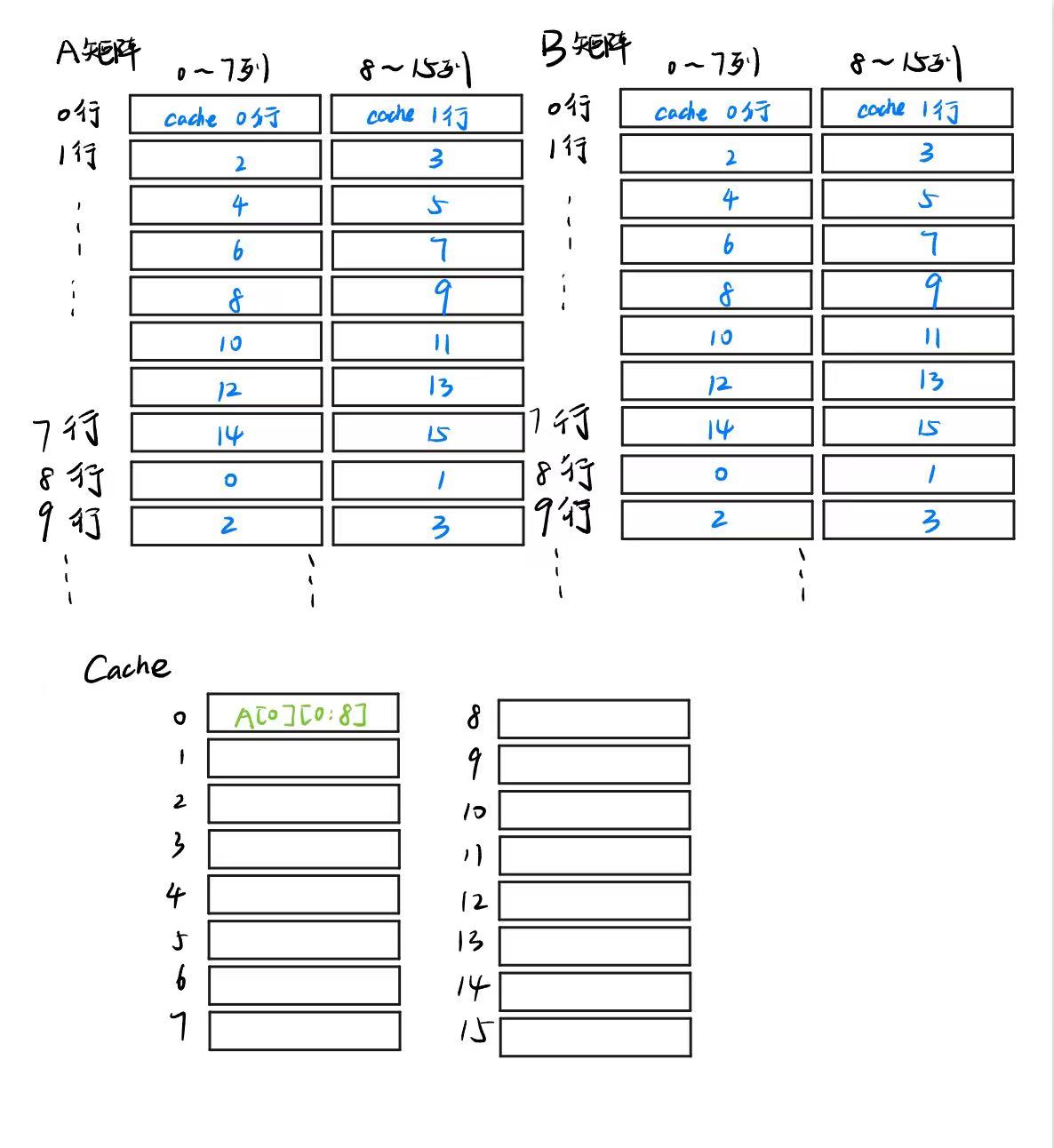

然而，不仅读取A数组需要把A装进cache，赋值B数组的时候也要把B装进cache！

我们会把A[0][0]赋值给B[0][0],这时，也需要把B[0][0:7]的内容也装进cache，还记得吗，B[0][0:7]也只能映射到cache的第0行，此时miss次数+1，而且原来A装进cache第0行的内容也被清理掉了！

然后i = 0, j = 1,执行语句B[1][0] = A[0][1]，同样，我们这时候要去cache中找有没有A[0][1]，也就是寻找A[0][0:8]，然而，就在刚刚，我们的A数组的这八个元素已经被清掉了。

这就导致cache的次数再次加1。我们要重新把A[0][0:8]放在cache的第一行。再然后，我们继续执行循环，把A[0][1:8]分别赋值在B[1:8][0]上，接下来，再把B数组的对应元素放在cache里，这时这个cache就长成这样了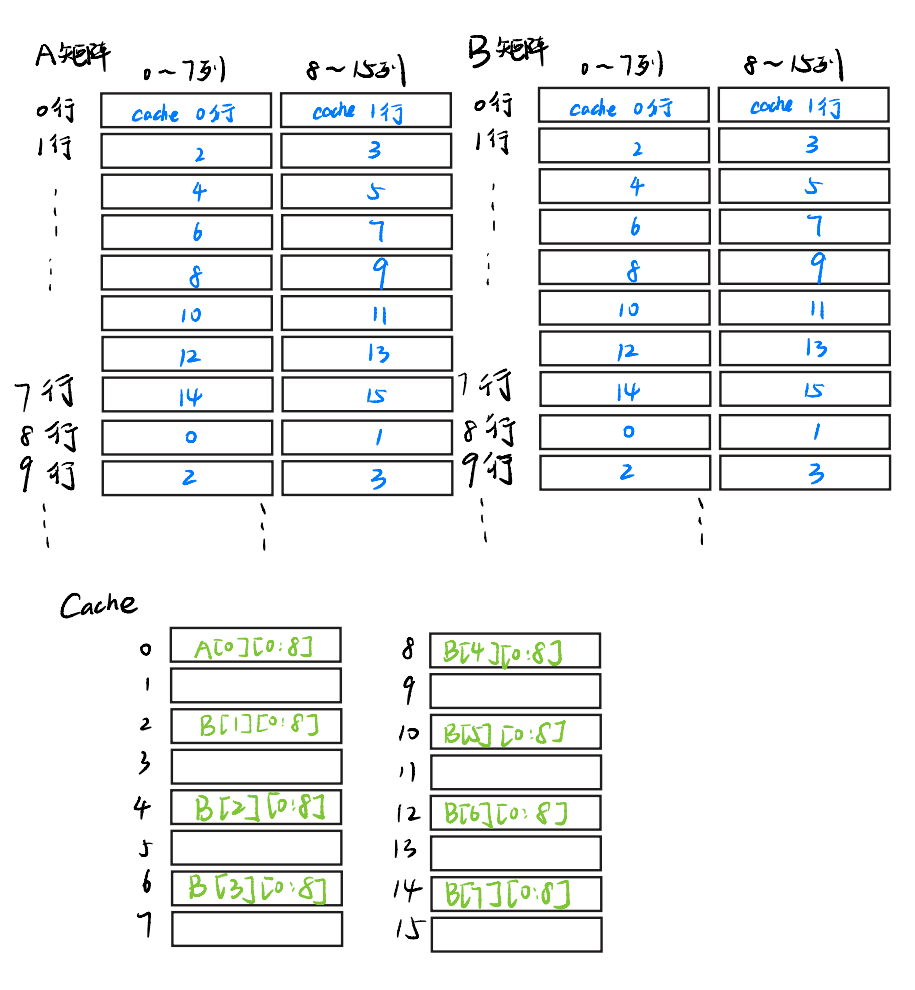

再然后，我们继续执行循环，要把A[0][9:16]赋值给B[9:16][0]，就在这时，我们首先把A[0][9:16]放进cache，按照映射关系放在了cache的第1行。

再然后，再把B数组的第8行到第15行的前八个元素都放进cache里。
这时，发现B数组的前8行的元素就都被新8行的元素替换掉了
此时cache变成了这样。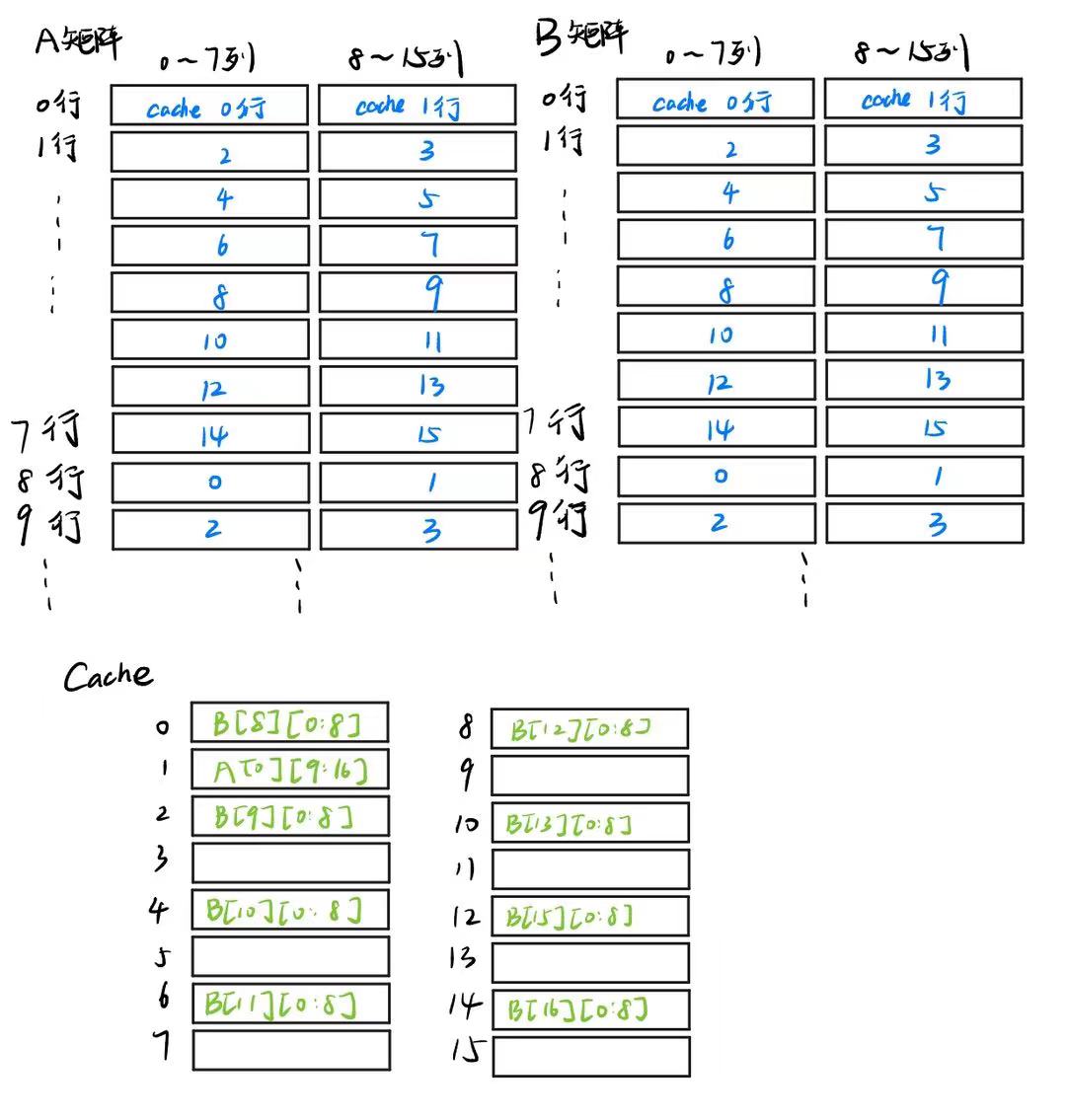

这样A[0][9:16]放进cache里，miss+1。B的八行替换，miss+8。

很好，这样第一行就替换完了。

随后i = 1,我们再次执行同样的操作。现在A[1][0:9]扔进cache里，按照映射关系扔进第二行，接下来，在把B[0][0:8] ~ B[7][0:8]都扔进cache里，替换了B的后九行的八个元素。cache又加8了。。。

等等，发现了什么😮，那这么说读到B[1][8:16]还有八次miss，B[2][0:8]还有8次miss······。那给每个B的元素赋值都有一次miss！

那岂不是单单给B赋值就需要16 * 16 = 256 次miss！这还没算读取A产生的miss，算了更大，不可能达到题目的<100次要求

那怎么办？

16 * 16矩阵分块策略

我们发现，上述做法的最大问题，就是B[0][i] ~ B[7][i]扔到cache的0,2,4,······14行之后，B[9][i] ~ B[15][i]会重新占据cache的0,2,4······14行，然后读B[0][i+1] ~ B[7][i+1]又会重新占据cache的0,2,4,······14行，导致cache疯狂miss

那怎么办？

其实只要我们先不读B[9][i] ~ B[15][i]，在把B[0][i] ~ B[7][i]放到cache之后并且赋值之后，直接赋值B[0][i+1] ~ B[7][i+1]，就不会产生多余的8次miss了！

也就是说，我们只需要把16 * 16的矩阵分成四个8 * 8矩阵，就可以避免大多数的miss了！

int i, j, k, t0, t1, t2, t3, t4, t5, t6, t7;
    for (i = 0; i < N; i += 8){
        for (j = 0; j < M; j += 8){
             for (k = i; k < i + 8; k++){
                    t0 = A[k][j];
                    t1 = A[k][j+1];
                    t2 = A[k][j+2];
                    t3 = A[k][j+3];
                    t4 = A[k][j+4];
                    t5 = A[k][j+5];
                    t6 = A[k][j+6];
                    t7 = A[k][j+7];
  
                    B[j][k]   = t0;
                    B[j+1][k] = t1;
                    B[j+2][k] = t2;
                    B[j+3][k] = t3;
                    B[j+4][k] = t4;
                    B[j+5][k] = t5;
                    B[j+6][k] = t6;
                    B[j+7][k] = t7;
             }
        }
    }

哇喔，就是这样，我们拿下了16 * 16矩阵的分数！

注意到，我上面用了t0~t7的变量，为什么要用这些而不直接把A的值赋给B呢
实际上这些变量都是寄存器，我们可以把A数组的值暂存到寄存器里，然后再赋给B

还记得上面写的这些内容吗

理解了上述映射的内容，我们就可以分析刚才的那段代码了，首先，当i = 0, j = 0时，会先访问A[0][0],这样，他就会把A[0][0:8]全部扔到cache的第0行，miss次数变成了1。

然而，不仅读取A数组需要把A装进cache，赋值B数组的时候也要把B装进cache！

我们会把A[0][0]赋值给B[0][0],这时，也需要把B[0][0:7]的内容也装进cache，还记得吗，B[0][0:7]也只能映射到cache的第0行，此时miss次数+1，而且原来A装进cache第0行的内容也被清理掉了！

然后i = 0, j = 1,执行语句B[1][0] = A[0][1]，同样，我们这时候要去cache中找有没有A[0][1]，也就是寻找A[0][0:8]，但是，就在刚刚，我们的A数组的这八个元素已经被清掉了。

这就导致cache的次数再次加1。我们要重新把A[0][0:8]放在cache的第一行。再然后，我们继续执行循环，把A[0][1:8]分别赋值在B[1:8][0]上，接下来，再把B数组的对应元素放在cache里，这时这个cache就长成这样了

如果我们先把A[0][0:8]的值都放进8个寄存器里，这样就不需要再重新把A[0][0:8]重新再放到cache的第一行了，直接把寄存器的值赋给B就行了，这样又少了几次miss，不错不错😊

然而，我们32 * 32矩阵的miss次数还是在惊人的1155次，举例AC相差甚远。

怎会如此？

32 * 32矩阵分块策略

我们需要先分析为什么16 * 16的分块策略不适用于 32 * 32
实际上，我们把A和B两个矩阵的映射关系写清楚就好理解了

同样，我们把A[0][0:8]先扔到cache里，再存到t0~t78个寄存器中，然后我们再以此把B放到cache中
B[0][0:8] ~ B[3][0:8]放在了cache的0,4,8,12行，嗯~4次miss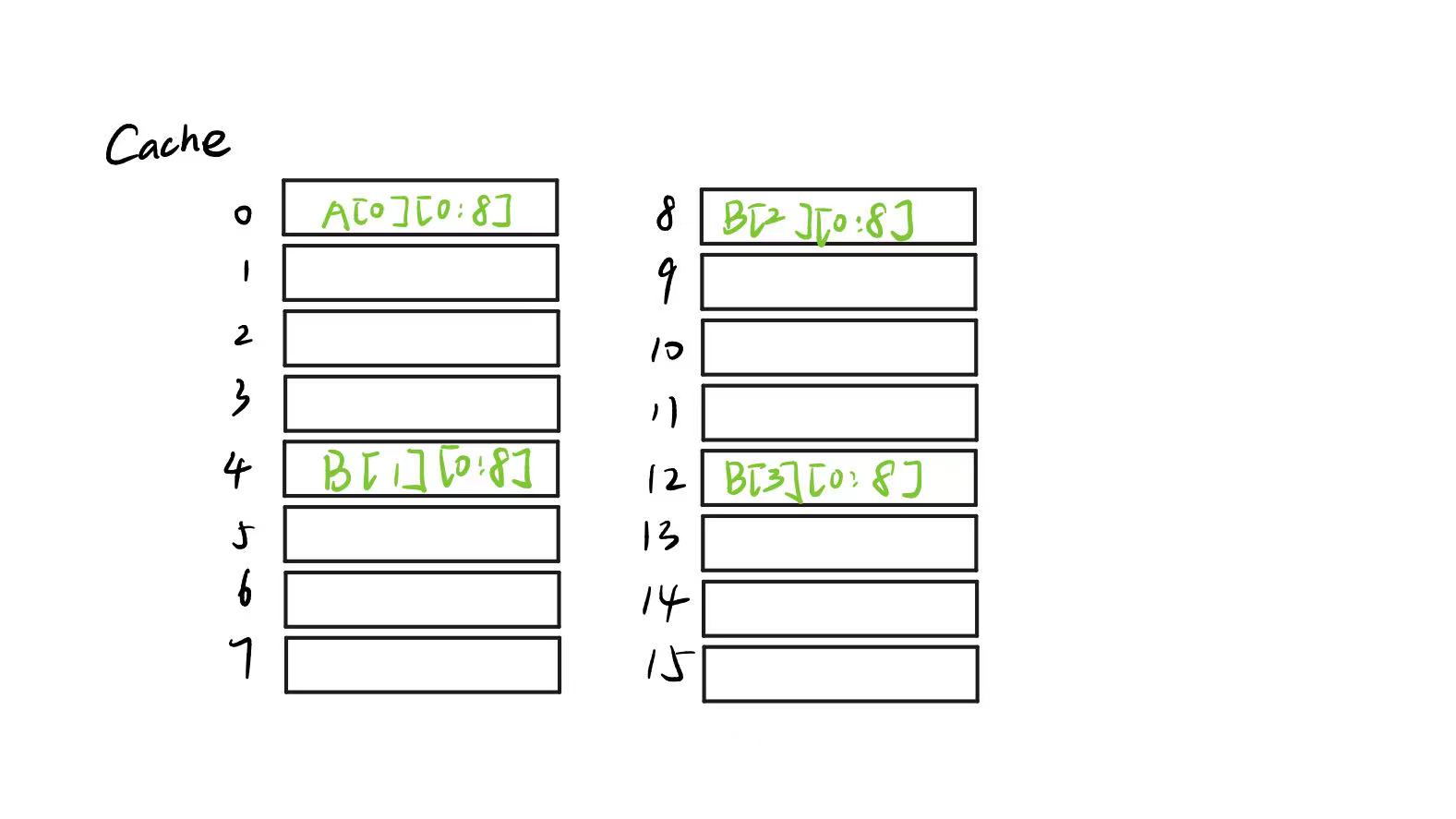

接下来再放B[4][0:8] ~ B[7][0:8]，发现，按照映射关系，他们会把B[0][0:8] ~ B[3][0:8]都挤出去。

再然后，把A[1][0:8]扔到cache里，再存到8个寄存器里。随后，为了给B[0][1] ~ B[3][1]赋值，我们又要把他们扔到cache的0,4,8,12行

这一幕似曾相识😮，最开始写的直接转换似乎就是出现了这个类似的问题才导致疯狂的miss。
那怎么办呢，难道要用更小的矩阵？用4 * 4的？

可是，cache的一行能存8个int，4 * 4分块是不是有些屈才？
实际上，4 * 4的分块方式会导致A矩阵和B矩阵都出现较多的miss（留给你思考。

不过miss数也大大减少，我们向着胜利迈出了很大的一步！

其实说，我们有更好的复杂，只不过有亿点方法🤔

以下内容有些抽象🤔

我们这里以非对角线上的矩阵为例

我们稍微更改了一下图，这里我们以把A[0][8:16]转置到B[8:16][0]为例，蓝字表示数组能映射到cache中的位置，那么初始状态下，矩阵和cache长这样

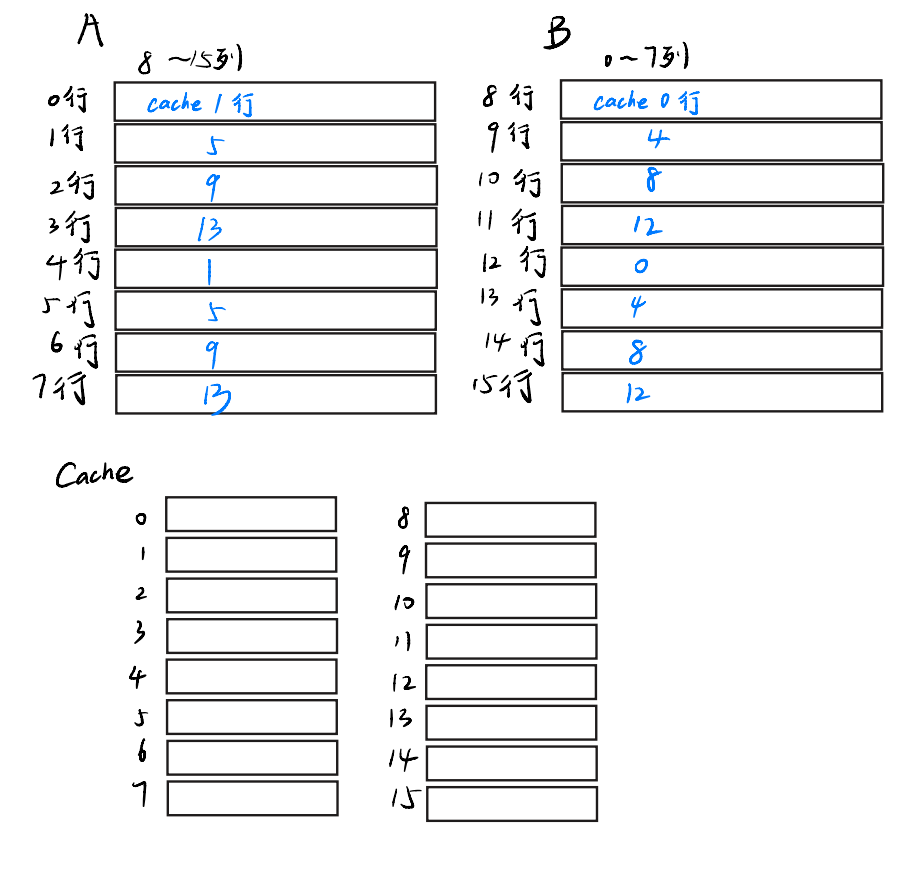
接下来，我们先把A[0][9:16]装进cache，把的前四行装进cache，并且直接赋值，那么cache变成了这样

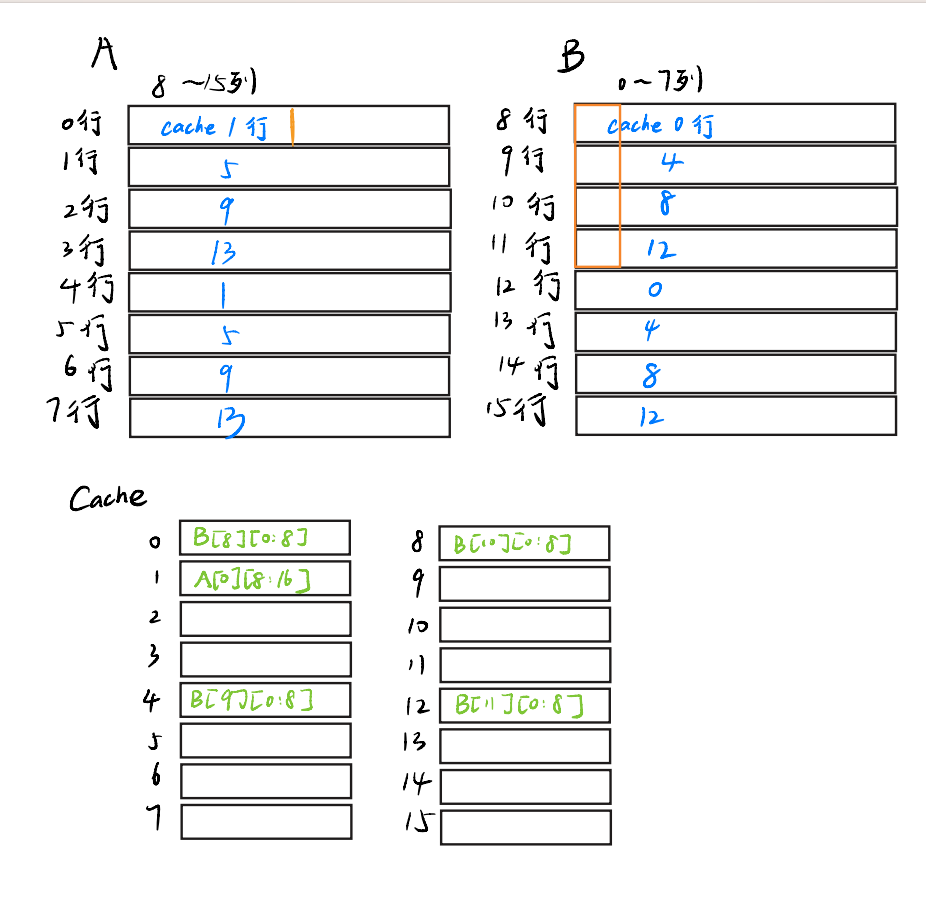
橙色表示：转置之后结果正确的元素

但是！我们先不赋值B[12:16][0],这样会把B的前四行顶掉，太浪费了。但是！我们A的后4个元素也别闲着，我们把它转移到B[8:12][4]去！这样，我们就再也不用访问A[0][8:16]了，即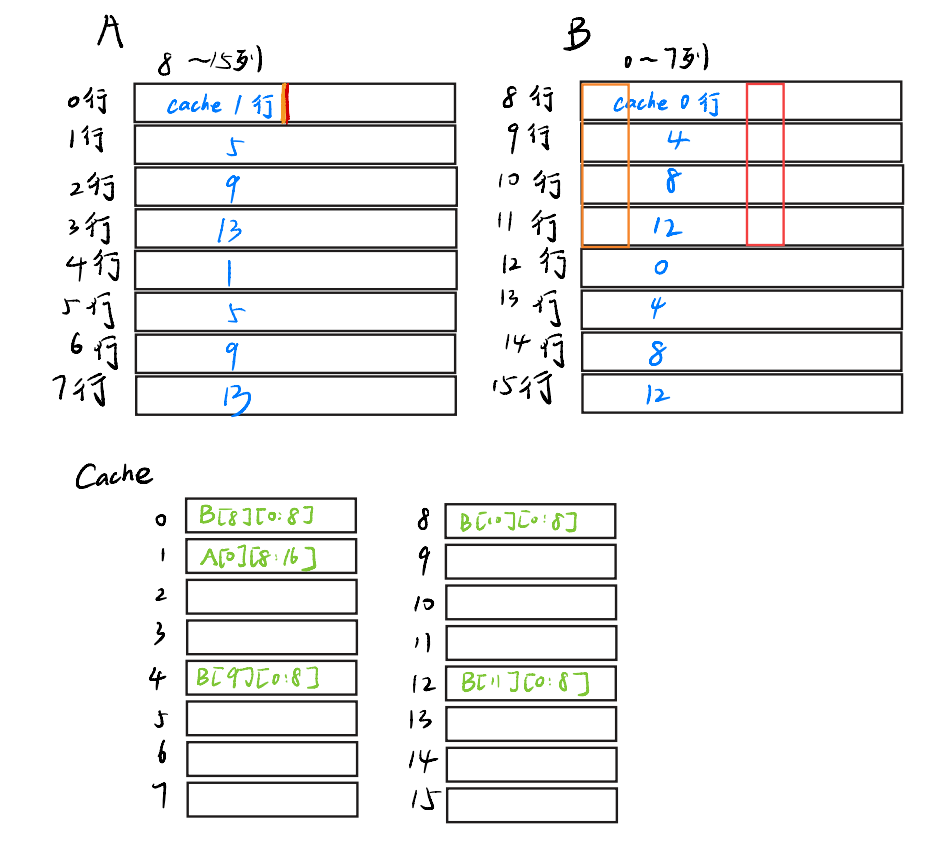

B中红色表示已被转移但是顺序不对的元素~

上述操作，我们一共有A的miss1次，B的miss四次~

接下来，我们把A的前4行都进行这个操作，这样A的总miss次数达到了4次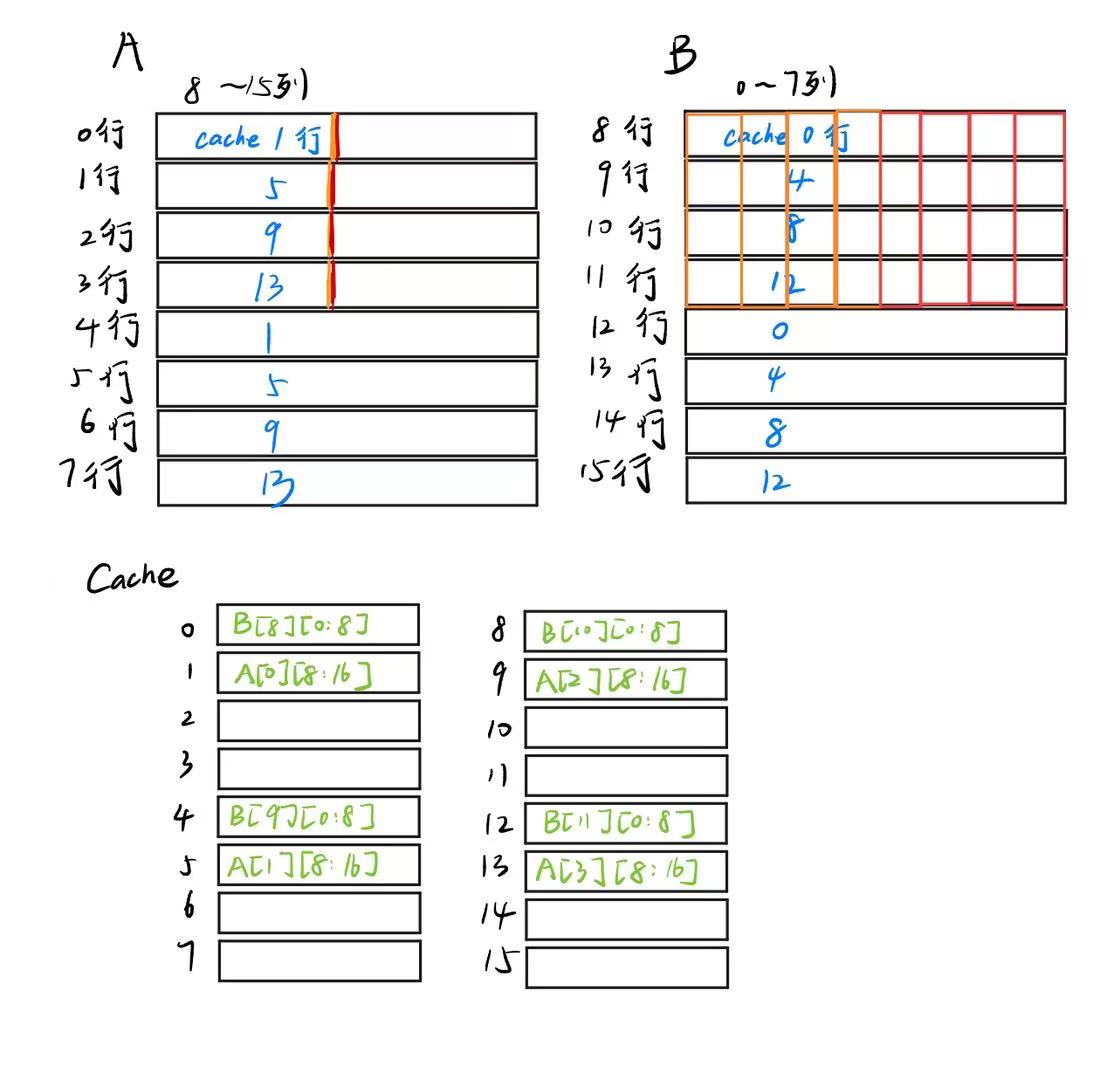

cache变成了这样~

接下来，我们把B[8][4:8]的值放进t0~t3的四个寄存器里，把A[4:8][0]放到t4~t7四个寄存器里，前一步不需要动cache，而后一步会把A的前4行扔出cache。A的前四行已经没用了，直接扔掉扔掉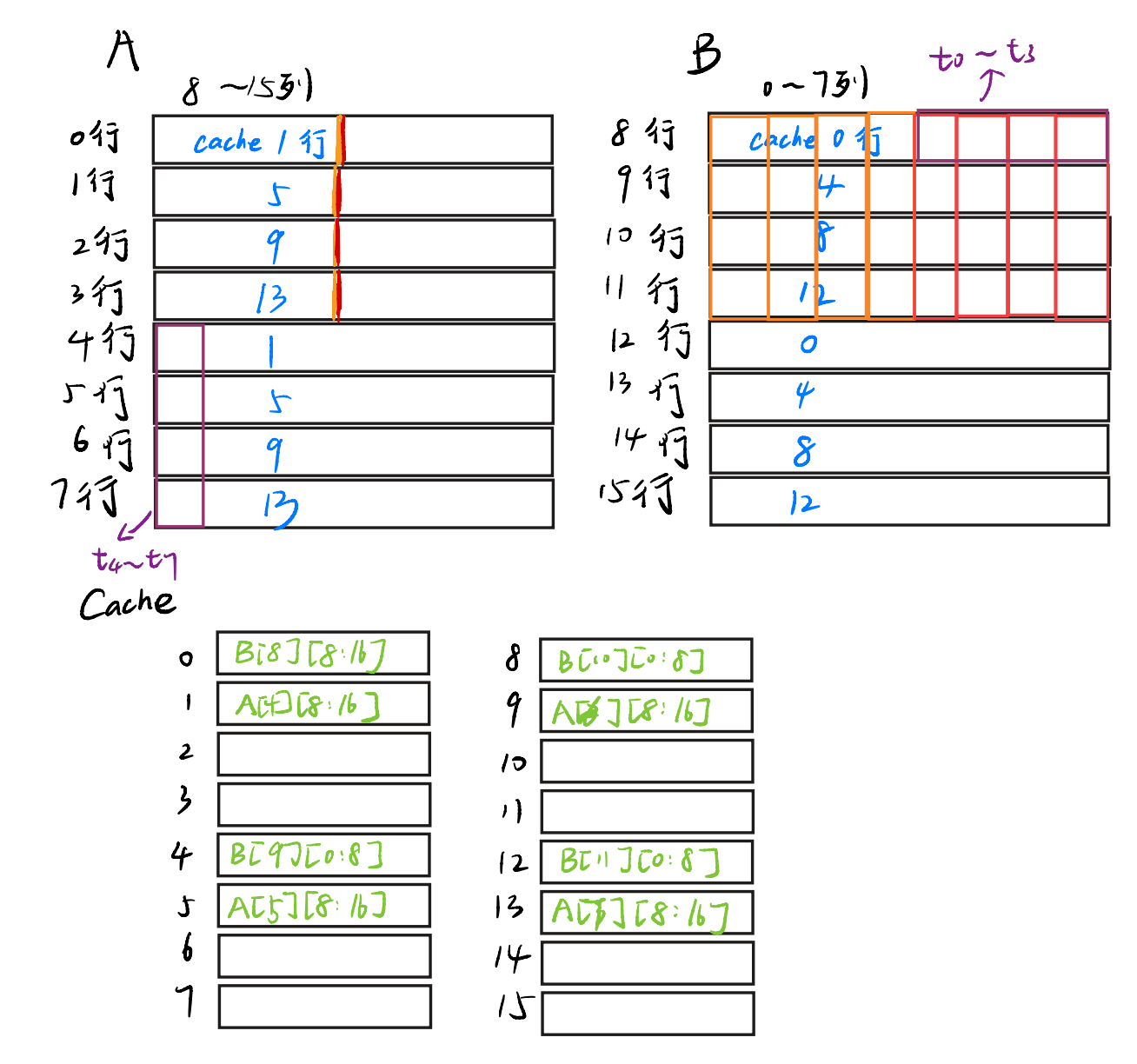

紫色表示被扔到寄存器里的值~

现在，我们的目的是，把t4~t7,t0~t3放进B的正确位置！我们刚刚把B[8][4:8]的元素都放进寄存器里了，这样的话，我们只需要先把t4~t7扔上去，就再也不需要把访问B[8][0:8]了！

所以我们先把t4~t7扔放到B[8][0:8]，这一步没有导致miss，然后，再把t0~t3的值放到B数组的正确位置，即B[12][0:4]，这一步我们把B的12行装进了cache~

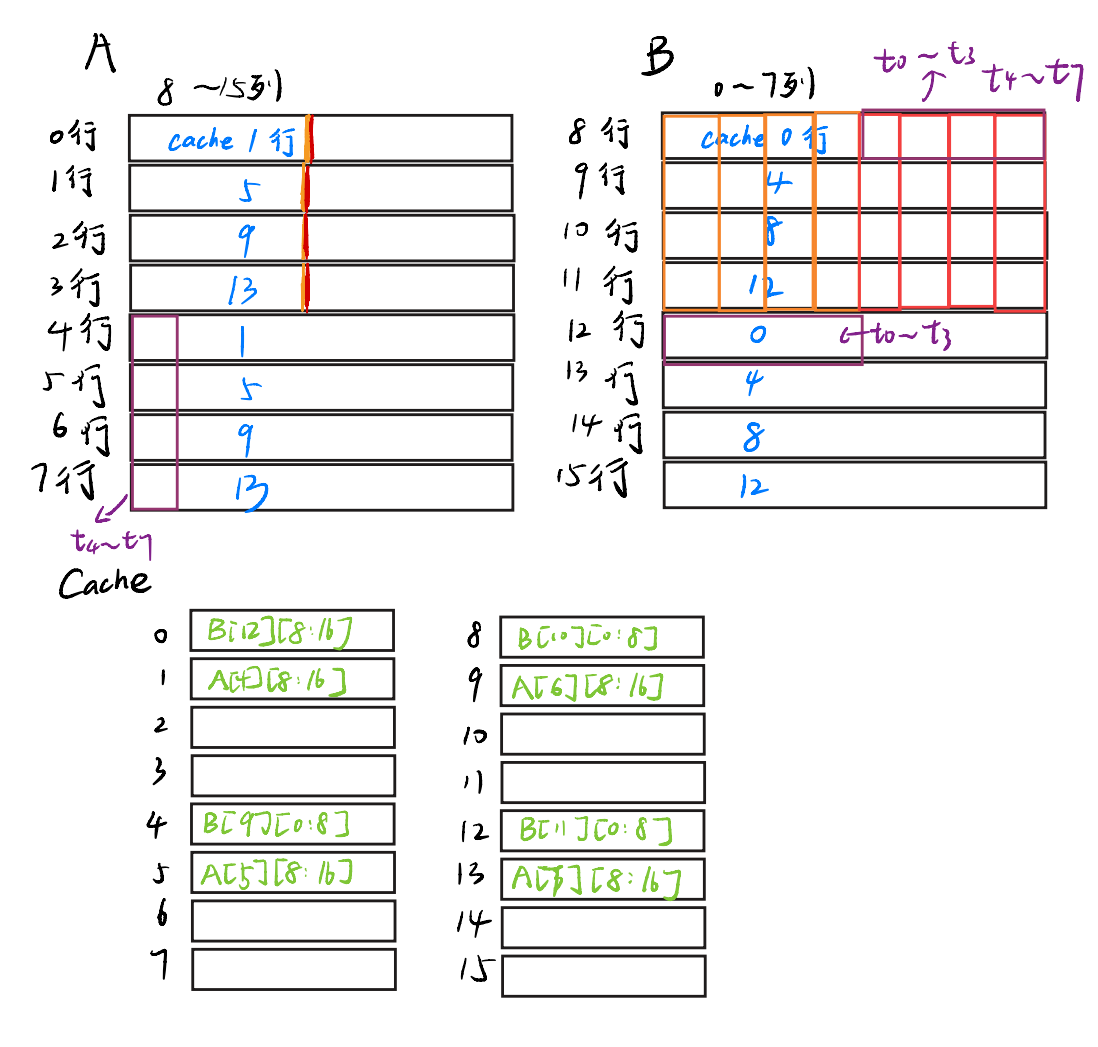
就像这样~，这样B[8]就排好了！

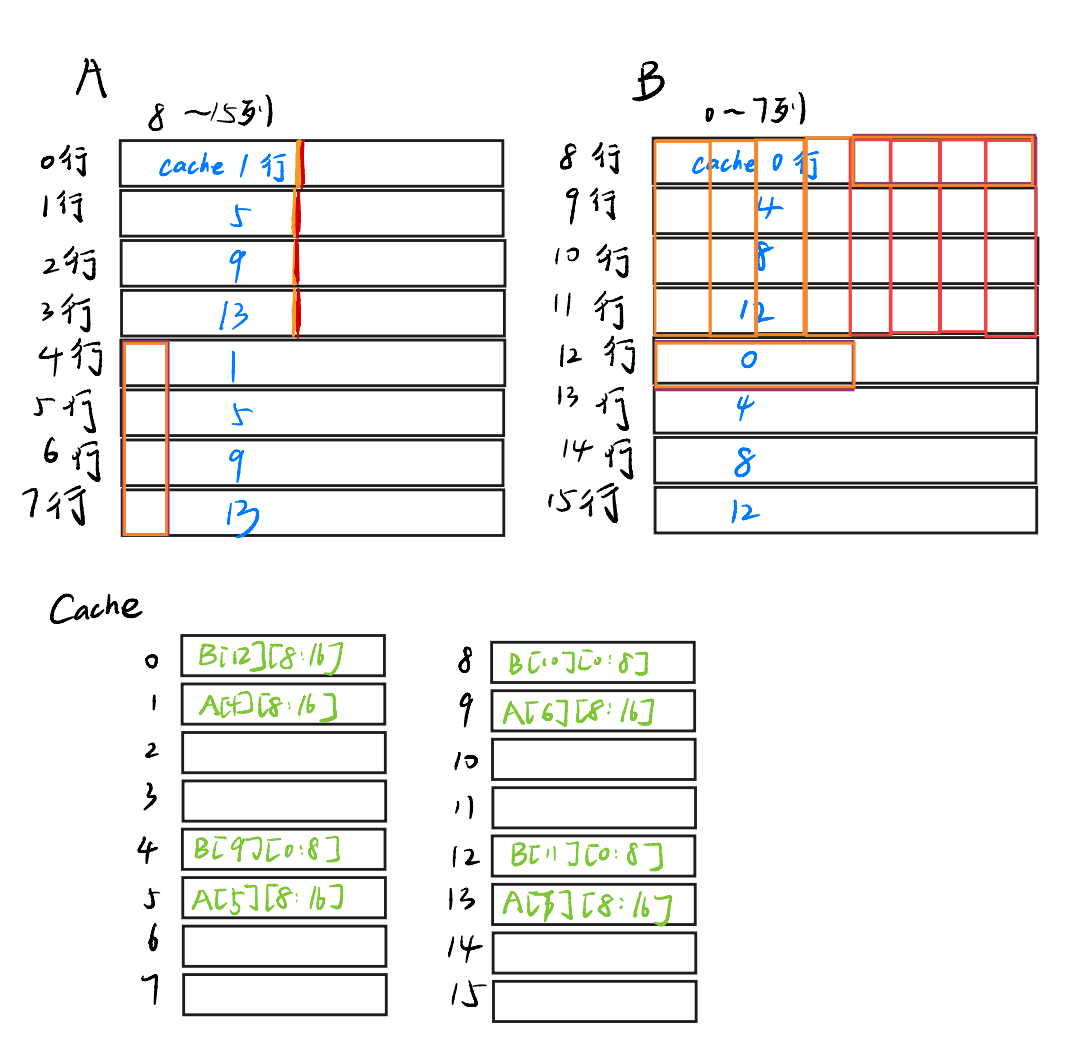
ps:橙色表示排好了

现在我们把A的4到7行和B的12行都装进cache了，那就顺手把12行的后4个元素装进去吧，反正也不会增加miss（因为A[4][0:8]~A[8][0:8]一直在cache呢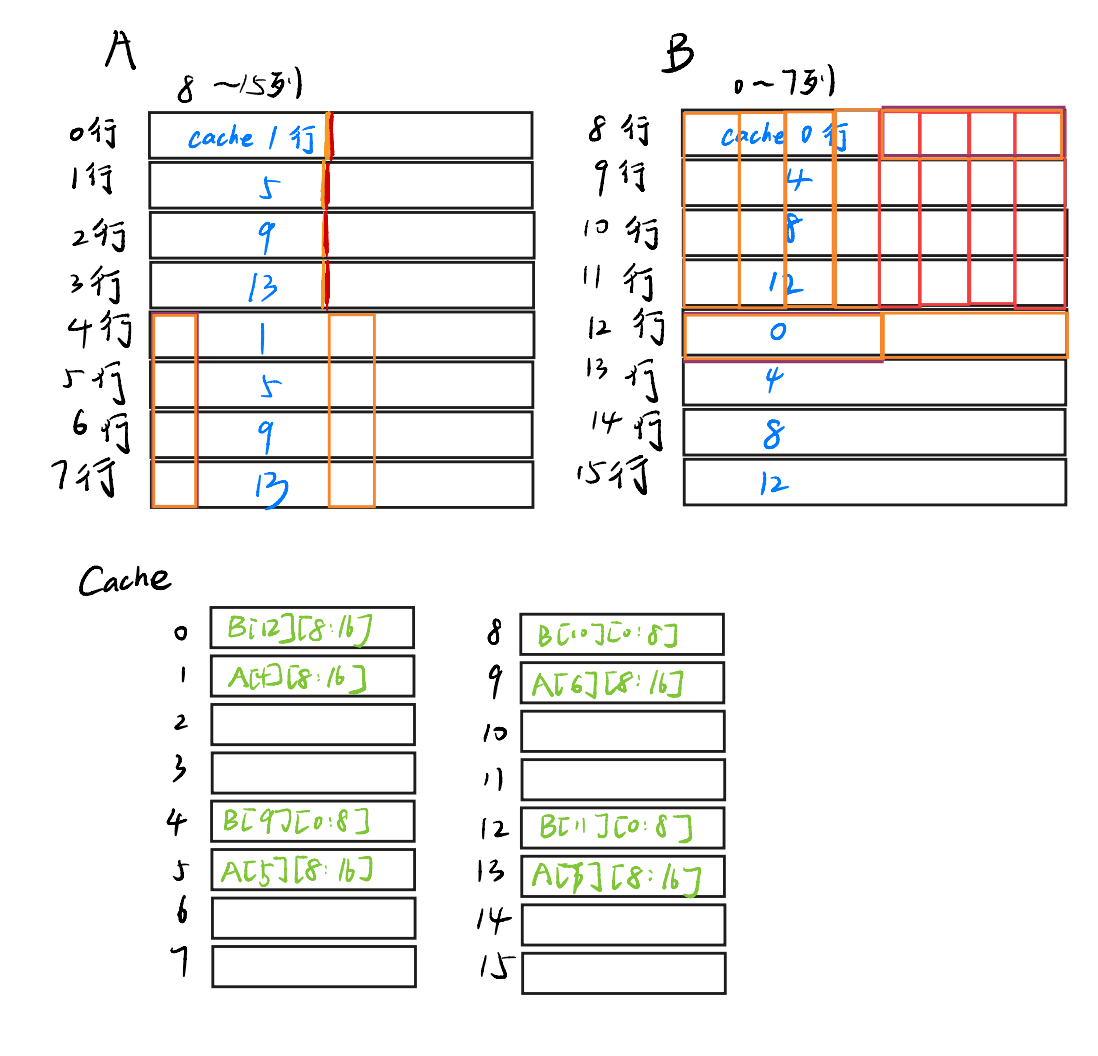

哇喔！这样，我们组装好了8 * 8 矩阵右上角的第一行，以及整个12行。

接下来，我们仿照刚才的操作，装好B第9行的右半部分和整个13行······就可以把整个8 * 8矩阵装好了！但是这些操作，都没有使得A矩阵miss，并且也只是让了B的第k+4行替换了B的第k行，每次也只会增加1次miss——

所以，以上操作已经很可以使得miss数尽量小了！

这是非对角线的情况，在对角线上，因为A可能和B的位置冲突，所以miss数会增加！但是我们也尽可能保证了低的miss数

下面是AC代码（小心查重——）

int i, j, m, t0, t1, t2, t3, t4, t5, t6, t7;
   if (M == 16)  
   {
       for (i = 0; i < N; i += 8)
           for (j = 0; j < M; j += 8)
               for (m = i; m < i + 8; m++)
               {
                   t0 = A[m][j];
                   t1 = A[m][j+1];
                   t2 = A[m][j+2];
                   t3 = A[m][j+3];
                   t4 = A[m][j+4];
                   t5 = A[m][j+5];
                   t6 = A[m][j+6];
                   t7 = A[m][j+7];

                   B[j][m]   = t0;
                   B[j+1][m] = t1;
                   B[j+2][m] = t2;
                   B[j+3][m] = t3;
                   B[j+4][m] = t4;
                   B[j+5][m] = t5;
                   B[j+6][m] = t6;
                   B[j+7][m] = t7;
               }
   }
   else if (M == 32)
   {
       for (i = 0; i < 32; i += 8)
       {
           for (j = 0; j < 32; j += 8)
           {
               for (m = 0; m < 4; m++)
               {
                   t0 = A[i+m][j];
                   t1 = A[i+m][j+1];
                   t2 = A[i+m][j+2];
                   t3 = A[i+m][j+3];
                   t4 = A[i+m][j+4];
                   t5 = A[i+m][j+5];
                   t6 = A[i+m][j+6];
                   t7 = A[i+m][j+7];

                   B[j][i+m]   = t0;
                   B[j+1][i+m] = t1;
                   B[j+2][i+m] = t2;
                   B[j+3][i+m] = t3;


                   B[j][i+m+4]   = t4;
                   B[j+1][i+m+4] = t5;
                   B[j+2][i+m+4] = t6;
                   B[j+3][i+m+4] = t7;
               }

               for (m = 0; m < 4; m++)
               {

                   t0 = B[j+m][i+4];
                   t1 = B[j+m][i+5];
                   t2 = B[j+m][i+6];
                   t3 = B[j+m][i+7];


                   t4 = A[i+4][j+m];
                   t5 = A[i+5][j+m];
                   t6 = A[i+6][j+m];
                   t7 = A[i+7][j+m];

                   B[j+m][i+4] = t4;
                   B[j+m][i+5] = t5;
                   B[j+m][i+6] = t6;
                   B[j+m][i+7] = t7;


                   B[j+m+4][i]   = t0;
                   B[j+m+4][i+1] = t1;
                   B[j+m+4][i+2] = t2;
                   B[j+m+4][i+3] = t3;


                   t4 = A[i+4][j+m+4];
                   t5 = A[i+5][j+m+4];
                   t6 = A[i+6][j+m+4];
                   t7 = A[i+7][j+m+4];

                   B[j+m+4][i+4] = t4;
                   B[j+m+4][i+5] = t5;
                   B[j+m+4][i+6] = t6;
                   B[j+m+4][i+7] = t7;
               }
           }
       }
   }

提交，成功AC

不过，这种分块策略不是最优的，还可以再思考一下怎么继续降低miss数从而拿到Excellent（（

不过我不行了拿到分跑了跑了跑了——